ELFT HÍRADÓ

[György Szondy <gyorgy.szondy AT gmail.com>]

Tisztelt Lista tagok!

Az Általános Relativitáselmélet mindenképpen ingoványos talaj. Ahogy Abonyi
Iván egy 20 évvel ezelőtti levelében írta: sokan művelik, de kevesen értik.

Még nehezebb mindezt az ismeretterjesztés szintjére korrekt módon
leegyszerűsíteni. Nagy bátorság kell hozzá... láhatólag így sikerült.
Szóval abszolút megértem Szabados László helyesbítésre tett erőfeszítését.
És matematikailag kétségtelenül helyes is amit leírt.

Ugyanakkor (7 év után) ismételten fel kell hívnom a figyelmet Hermann Weyl
1917-es On the Theory of Gravitation című cikkére [Ann. d. Physk, 54, 117,
(1917)] melyben kifejti, hogy a Schwarzschild fekete-lyuk geometriája
megfelelő koordinátázás mellett (izotrop koordinátákra való áttéréssel)
természetes módon úgy terjeszthető ki, hogy míg az r>r_s (eseményhorizonton
kívüli) tartományt 2x fedi le, az r<r_s tartományt egyáltalán nem. (Ezzel a
levezetéssel egyébként már a Landau II. 100§ 4. feladatban is
találkozhattunk. Csodálom, hogy nem közismert. Sőt.)

Ezzel a levezetéssel Wely gyakorlatilag 1917-ben, matematikailag definiálta
az Einstein-Rosen-féle féreglyukat. (Persze mivel negatív frekvencia nem
létezik, a belső univerzumban sem visszafelé fog telni az idő.)

[Ennek értelmében az eseményhorizontnál nem úgy esünk bele egy fekete
lyukba, ahogy ezt általában el szokták képzelni, hanem gyakorlatilag
átesünk egy másik (belső) univerzumba: a kint és bent fogalma
felcserélődik, és tovább megyünk ugyanabba az irányba, mégis látszólag
távolodni fogunk az eseményhorizonttól.]

Weyl levezetése alapján az, hogy a fekete lyuk belsejében ( r<r_s
koordináták esetén) a tér időszerűvé válik igazából pusztán egy matematikai
megoldás. Mintha a valós számok halmazán a -1 négyzetgyökét szeretnénk
értelmezni. A fentiek értelmében ugyanis az r<r_s tartomány nem része
Schwarzschild megoldás értelmezési tartományának, vagyis nem része a
fizikai valóságnak/ a való világnak.

Szavazásra nem bocsátanám a dolgot, mert a tudomány nem szavazáson múlik.
De arra kíváncsi lennék, hogy hányan néznek utána a hivatkozott cikknek,
vagy a Landau-ban lévő levezetésnek.

Üdvözlettel,
Szondy György

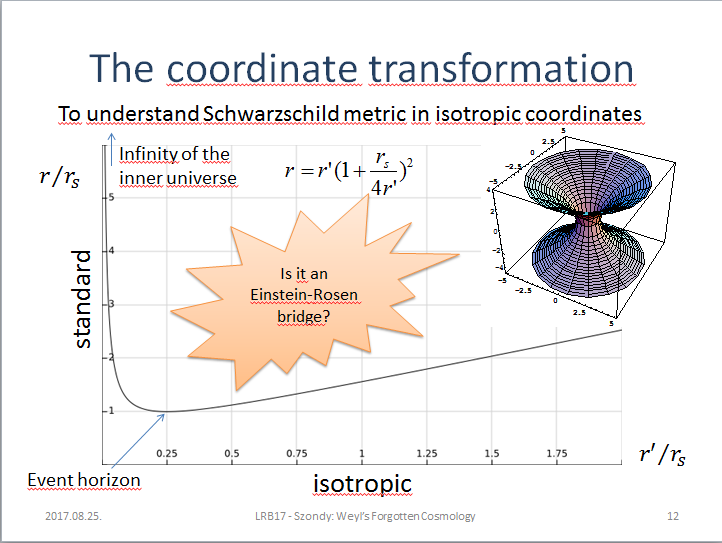
ui: a könnyebb megértés érdekében mellékelem az alábbi, a Weyl féle
koordináta-transzformációt magyarázó ábrát.

[image: kép.png]




On Tue, Feb 16, 2021 at 3:38 PM Szabados,L. <lbszab AT rmki.kfki.hu> wrote:

> *-----------------------------------------------------------------------*
> |                        E L F T   H I R A D O                          |
> |       Az Eotvos Lorand Fizikai Tarsulat informacios es vita-lapja     |
> |-----------------------------------------------------------------------|
> |  Az ELFT adoszama (ide kerjuk az SZJA 1 szazalekat!):  19815644-2-43  |
> |-----------------------------------------------------------------------|
> |   A megjelent cikkek tartalmaert teljes egeszeben bekuldojuk felelos. |
> *-----------------------------------------------------------------------*
>
>
> T. Lista!
>
> A 2020 évi fizikai Nobel dij kapcsán a hazai ismeretterjesztő irodalomban
> több cikk is megjelent (ill. vélekedés kapott nyilvánosságot az
> elektronikus sajtóban). A megmosolyogtatóan naiv vagy bosszantóan
> dilettáns irások közül csillagászati szakmai igényességével toronymagasan
> emelkedik ki Kovács Józsefnek a Magyar Tudomány februári számában
> megjelent irása [1]. Ebben nagyon jól olvasható összefoglalását kapjuk a
> két dijazott csillagász kutató, Andrea Ghez és Reinhard Genzel
> eredményének (és az általuk használt technikának): hogy miért is lehetünk
> biztosak abban, hogy a Tejútrendszer centumában egy kb. 4 millió
> Nap-tömegű fekete lyuk van.
>
> A cikk Roger Penrose immár klasszikus, az általános relativitáselmélet
> első modern szingularitástételét publikáló [2] cikkének az ismertetése és
> jelentőségének a bemutatása azonban egy kissé problematikusnak látszik,
> mégpedig két okból.
>
> 1. A Schwarzschild fekete lyuk kapcsán azt olvassuk, hogy `A
> Schwarzschild-téridőben az eseményhorizontot sugárirányban befelé átlépve
> a tér és az idő szerepet cserél, és a gömbi koordinátákban a középpont
> felé mutató "befelé" az idő lesz.' A probléma az, hogy ez az állitás nem
> igaz. De nem is érdemelne ez a korrigálandó mondat különösebb figyelmet,
> ha ez nem jelent volna meg ugyanigy a Fizikai Társulat ismeretterjesztő
> lapjának a novemberi számában, ugyancsak a 2020-as fizikai Nobel dij
> kapcsán. (Itt további, a fekete lyukak tulajdonságaira vonatkozó
> meglehetősen zavarba ejtő megállapitás mellett még ráadásul szép szines
> ábrán illusztrálva is van, hogy a lyukon kivül `tér', azon belül meg `idő'
> van. Tehát úgy tűnik, hogy nem csupán szerencsétlen megfogalmazásról,
> hanem egy, a koordináták szerepének a félreértéséről van szó.)
>
> 2. Nem derül ki, hogy mi a tényleges jelentősége Penrose cikkének a fekete
> lyukak elméletében: Nem az, hogy az adott feltételek mellett
> szingularitások alakulnak ki (hiszen hogy mi van a horizonton belül, az a
> külső megfigyelő számára és a horizonton kivüli világ folyamatai
> szempontjából -- a lyuk gravitációs `erőterének' a dipólnál magasabb
> rendű és gyorsan lecsengő multipól momentumain túl -- irreleváns); de nem
> is az, amit más helyen olvashatunk, miszerint `bebizonyitotta, hogy az
> általános relativitáselmélet szerint a gravitációs összeomlás
> eredményeként fekete lyukak jönnek létre'. Nem, a dijazott cikkben nem azt
> bizonyitotta be.
>
> A jelen irásunk célja, hogy korrigáljuk (ill. pontositsuk) az 1. pontban
> emlitett hibás állitást, rámutatva arra, hogy mi lehet a félreértés oka;
> és hogy egy korrekt összefoglalását adjuk Penrose hires cikkének és
> világosan lássuk annak tényleges jelentőségét a fekete lyukak fizikájában.
>
> %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
>
> 1. Tehát igaz-e, hogy `A Schwarzschild-téridőben az eseményhorizontot
> sugárirányban befelé átlépve a tér és az idő szerepet cserél, és a gömbi
> koordinátákban a középpont felé mutató "befelé" az idő lesz'?
>
> Nem, egyáltalán nem. Ezért a fenti állitást korrigálandó/pontositandó,
> először foglaljuk össze, hogy honnan is jönnek a $(t,r,\theta,\phi)$ ún.
> Schwarzschild koordináták.
>
> A Schwarzschild téridőnek négy metrikus szimmetriája van: a gömbszimmetria
> (3 generátorral) és egy olyan szimmetria, ami az aszimptotikusan sik
> tartomány sztatikusságát eredményezi. E generátorok, amik vektormezők a
> téridősokaságon, természetesen Lie algebrát alkotnak, és ebben ez utóbbi
> szimmetria generátora, jelöljük ezt $K$-val, kommutál a gömbszimmetria
> három generátorával. (Régebben a diákjaimnak mindig feladtam házi
> feladatként, hogy bizonyitsák be, hogy bármely olyan négy dimenziós
> valós Lie algebra aminek az $so(3)$ rész Lie algebrája, szükségképpen
> direktösszeg: $so(3) \oplus I$. Igy az $I$ elemei mindig kommutálnak az
> $so(3)$ elemeivel, függetlenül attól, hogy e generátorok most épp
> vektormezők.) A gömbszimmetriát generáló vektormezők mindenütt térszerűek,
> de a $K$ vektormező kauzális jellege a téridősokaság különböző
> tartományain más és más: $K$ az eseményhorizonton kivül *időszerű*, de a
> horizonton *fényszerűvé*, a horizont mögött pedig *térszerűvé* válik. A
> $(t,r,\theta,\phi)$ koordináták a fenti szimmetriagenerátorokhoz vannak
> illesztve; s hogy ezek a koordináták igy bevezethetők, a gömbszimmetria
> generátorainak és a $K$-nak a kommutálása teszi lehetővé. Speciálisan, a
> $t$ koordináta a $K$ integrálgörbéi menti természetes paraméter,
> *függetlenül* a $K$ kauzális jellegétől. A horizont mögött tehát $t$ már
> *térszerű* görbék természetes paramétere, merthogy ott a $K$ már térszerű.
> Abból, hogy a horizonton kivül $t$ `időkoordináta' (meghogy $t$-vel
> jelöltük), még nem következik, hogy az a horizonton belül is az `idővel'
> kell, hogy kapcsolatos legyen. Igy aztán a horizont átlépése során a $t$
> `térszerű' (és az $r$ `időszerű') *koordinátává* válásából a `tér'-re és
> az `idő'-re semmi (és igy speciálisan azok `felcserélődése') sem
> következik. Csak a *koordináták* kauzális jellege változik.
>
> Az `idő' és a `tér' ui. *nem* cserélődik fel a horizonton való áthaladás
> során, mivel azt, hogy mi az idő- ill. térirány, minden pontban a *lokális
> fénykúpok* mondják meg: egy irány időszerű és jövő/múlt irányitott, ha az
> a lokális jövő/múlt fénykúp belsejébe mutat, és térszerű, ha azon kivülre.
> Mivel a fénykúpok a téridősokaságon folytonosan (sőt, a Schwarzschild
> geometriában analitikusan!) változnak, az idő- ill. térirányok fogalmában
> semmiféle nem folytonos, ugrásszerű változás sem állhat elő. Ez jól
> látszódik, ha a metrikát pl. az avanzsált Eddington--Finkelstein
> koordinátákban irjuk fel (ami a Minkowski téridő $(v,r,\theta,\phi)$
> avanzsált gömbi koordinátáival analóg), és amiben a horizont egy
> *reguláris, analitikus* fényszerű hiperfelület lesz és a lokális fénykúpok
> is e koordináták *analitikus* függvényeivel adhatók meg. A Penrose hires
> [2] cikkében található ábra is ebben a koordinátarendszerben mutatja be a
> gravitációs összeomlás folyamatát és a horizont és a szingularitás
> kialakulását.
>
> Ugyanakkor a $(v,r,\theta,\phi) --> (t,r,\theta,\phi)$
> koordinátatranszformáció Jacobi mátrixának a determinánsa a horizonton (és
> csak ott) zérus. A $(t,r,\theta,\phi)$ koordináták tehát *nem* globálisan
> jól definált koordináták, azok csak a $0 < r < 2m$ és a $2m < r < \infty$
> *diszjunkt, nyilt* tartományokon jól értelmezettek. Az egyik nyilt
> tartomány Schwarzschild koordinátái *nem* folytatásai a másik nyilt
> tartomány Schwarzschild koordinátáinak. A $(t,r,\theta,\phi)$
> koordinátarendszerek a horizonton *szingulárissá* válnak. Igy a
> koordináták egyik tartománybeli interpretációja sem vihető át
> automatikusan a másik tartományra. Hogy a horizonton a teljesen reguláris
> fénykúpok mennyire degeneráltnak *tűnnek* a Schwarzschild koordinátákban,
> jól mutatja a 23. ábra Hawking és Ellis klasszikus [3] monográfiájának a
> 152. oldalán. Talán egy ilyen ábra sugallhatta azt a téves képzetet, hogy
> a horizontot átlépve `az idő és a tér felcserélődik'.
>
> A Schwarzschild koordináták fenti viselkedése teljesen hasonló a Minkowski
> téridőben a kvantumtérelméleti Unruh effektus kapcsán megismert
> $(T,X,Y,Z)$ ún. Rindler koordináták viselkedéséhez. Mig a Minkowski téridő
> szokásos $(t,x,y,z)$ Descartes koordinátáit a téridő valamely időszerű
> transzlációs szimmetriát generáló vektormezőjéhez illesztjük, a Rindler
> koordinátákat pl. az $x$-irányú Lorentz-boostokat generáló vektormezőhöz,
>
> $K = x (\partial/\partial t) + t (\partial/\partial x)$
>
> -hez adaptáljuk. A $T$ ezen vektormező integrálgörbéi menti természetes
> paraméter. Csakhogy, a Schwarzschild megoldásbeli $K$ vektormezőhöz
> teljesen hasonlóan, ez a vektormező sem mindenhol időszerű: $K$ időszerű
> az $x>\vert t\vert$ és $-x>\vert t\vert$ diszjunkt, nyilt tartományokon,
> fényszerűvé válik a $t=\pm x$ fényszerű hipersikokon, és térszerű a
> $t>\vert x\vert$ és $-t>\vert x\vert$ nyilt tartományokon. (A könnyebb
> érthetőség kedvéért javasoljuk a kedves olvasónak e tartományok
> lerajzolását egy papirlapra.) Ez utóbbi két tartományon tehát a $T$
> koordináta *térszerű* integrálgörbék természetes paramétere, miközben az
> az előbbi kettőn még *időszerű* integrálgörbék paramétere. De ez alapján
> senki sem gondolná, mint ahogy ebből nem is következik, hogy a Minkowski
> téridő bizonyos tartományaiban `az idő és a tér szerepet cserél' (csak
> azért, mert a Descartes helyett a Rindler koordinátákat kezdtük el
> használni); pedig a helyzet pontosan ugyanaz, mint amit a Schwarzschild
> téridő kapcsán láttunk. Hasonlóan, a $T$ (idő)koordináta a $x>\vert
> t\vert$ tartományon a $t$ időkoorninátának monoton *növekvő*, de a
> $-x>\vert t\vert$ tartományon már monoton *csökkenő* függvénye. De ebből
> nem következik, hogy a Minkowski téridő bizonyos tartományaiban `az idő
> visszafelé telik'.
>
> Hogy tehát mi a tér- és időirány, és hogy az utóbbiak közül melyik a jövő
> és melyik a múlt, a fekete lyukak belsejében is a lokális fénykúpok
> mondják meg, és nem a koordináták. Ugyanakkor, a Schwarzschild megoldásban
> a $0 < r < 2m$ tartomány valóban különös tulajdonságokkal rendelkezik.
> Például, hogy egy tetszőleges ottani pontból inditott részecske (akár
> massziv, akár zérus tömegű) *véges* sajátidőn/affin paraméterhosszon belül
> *kikerülhetetlenül* belezuhan a centumba, és ennek a sajátidőnek/affin
> paraméterhossznak a lehetséges maximális értékét a lyuk tömege és a
> részecske kezdeti poziciója meghatározza. Hogy az $r=2m$ fényszerű
> hiperfelület `eseményhorizont'-ként jelenik meg ennek a ténynek a
> következménye, mert az $r=2m$ hiperfelület az emlitett tulajdonsággal
> rendelkező pontok halmazának a *határa*.
>
> A másik figyelemre méltó különlegessége a $0 < r < 2m$ tartomány
> geometriájának, hogy a $K$ szimmetriagenerátor térszerűvé válása miatt e
> tartományban az $r=const$, immár *térszerű* hiperfelületekben pl. bármely
> két $t=const$ ill. $t'=const$ sugarú gömbfelület felszine *azonos*, még
> akkor is ha pl. $t < t'$. Itt a téridőgeometria *homogén* (mint a
> kozmológiai modellekben), de már *nem stacionárius*.
>
>
> %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
>
> 2. Régóta ismert volt az a tény, hogy egy egzaktul gömbszimmetrikus anyag
> teljes gravitációs összeomlása során a centrumban szingularitás alakul ki.
> De ez nem meglepő, hisz ha a gravitációs összeomlás teljes (azaz a [nem
> porszerű] anyagban az egyre növekvő nyomás nem állitja meg az összeomlási
> folyamatot), akkor a gömbszimmetria miatt az anyag összes részecskéje a
> centrumba kell, hogy essen. Igy van ez a newtoni gravitációelméletben is.
> Csakhogy a Newton elméletben kialakuló szingularitás *nem stabil* abban az
> értelemben, hogy a gömbszimmetrikus anyageloszlás kicsi, de *nem*
> gömbszimmetrikus perturbációja már azt eredményezi, hogy az anyag
> részecskéi zömmel elkerülik a centrumot, és ott nem alakul ki semmilyen
> szingularitás. De egy *reális* összeomlási folyamat bizonyosan nem
> rendelkezik semmilyen *egzakt* geometriai szimmetriával. A Newton
> elméletben tehát a gömbszimmetrikus összeomási folyamatban kialakuló
> szingularitás `nem fizikai', annak megjelenése a magas fokú egzakt
> geometriai szimmetriák, nevezetesen a gömbszimmetria következménye.
>
> A kérdés tehát az, hogy az általános relativitáselmélet szerint is
> ugyanez-e a helyzet; azaz hogy a szimmetrikus (és analitikusan
> végigszámolható!) esetekben megjelenő szingularitás most is csupán a magas
> fokú egzakt geometriai szimmetriák következménye-e. A Landau iskolához
> tartozó Lifsic és Kalitnyikov perturbációs számolásai ez látszottak
> alátámasztani. De mivel az általános relativitáselmélet alapegyenletei,
> azaz az Einstein egyenletek erősen nemlineárisak, erős kétségek merültek
> fel a szokásos perturbativ módszerek megbizhatóságával, és a
> Lifsic--Kalitnyikov vizsgálatok konklúziójával kapcsolatban.
>
> De akkor hogyan dönthető el, hogy egy nem-szimmetrikus összeomlási
> folyamatban kialakul-e *fizikai* szingularitás? Van-e olyan matematikai
> módszer, amellyel biztonsággal eldönthető ez a kérdés? További, és még
> nehezebb probléma, hogy korábban amit fekete lyuknak lehetett nevezni, az
> mindig az Einstein egyenletek egy (gömb- vagy tengelyszimmetrikus) *egzakt
> megoldásában* jelent meg, és `mindenki tudta' hogy mi is a lyuk. De ha
> nincsenek ilyen szimmetriák és megoldások, akkor mit kell `fekete lyuk
> tartománynak' hivni; azaz mi a kritériuma annak, hogy egy adott téridő
> (azaz megoldása az Einstein egyenleteknek) fekete lyukat is tartalmaz?
> Másként fogalmazva: mi az az általános, mindenféle szimmetria lététől
> függetlenül matematikailag is jól definiált fogalom, amivel a fekete lyuk
> lényegi tulajdonsága megragadható, s amelyre alapozva a fekete lyukak
> tulajdonságaira vonatkozó állitások matematikailag is bizonyithatók és,
> lévén a fizika kvantitativ tudomány, *kvantitativ* összefüggések
> származtathatók?
>
> Mivel a korábbi perturbativ módszerek segitségével nem sikerült a kérdést
> eldönteni, új technikára/módszerre, esetleg paradigmaváltásra volt
> szükség. Egy ilyen paradigmaváltást eredményezett Penrose [2] cikke. Ez
> volt az a publikáció, amelyben először megjelent az a matematikailag is
> jól definiált fogalom, a zárt csapdázott felület fogalma, amivel a fekete
> lyukak lényege egzakt geometriai szimmetriáktól függetlenül is megfogható,
> és kvantitative is jellemezhető.
>
> Hogy e fogalom tartalmát világosan lássuk, vegyünk egy (nem feltétlenül
> gömbszimmetrikus) gömbi topológiájú felületet a közönséges 3 dimenziós
> térben, és inditsunk egy adott időpillanatban a felület minden pontjából a
> felületre merőleges irányokban egy fényjelet, mind kifelé mind befelé (a
> felület belsejébe). Ezek a fényjelek egy-egy hullámfrontot alkotnak, és
> azt, hogy hogyan terjednek a felülettől távolodva, az adott tér
> geometriája határozza meg. A sik 3 dimenziós térben a befelé induló
> fényjelek alkotta hullámfront felszine természetesen *monoton csökken*,
> mig, a várakozásainknak megfelelően, a kifele indulóké *monoton nő*.
>
> A zárt csapdázott felület a téridőben egy olyan zárt (pl. gömbi
> topológiájú) térszerű felület, hogy a róla merőlegesen nemcsak a befele,
> hanem a *kifele induló* fényjelek alkotta hullámfront minden egyes
> felületdarabjának a felszine is szigorúan monoton módon *csökken*. E
> fogalom nyilván független mindenféle szimmetriától, és stabil is (abban az
> értelemben, hogy kicsit deformálva a felületet és kissé megváltoztatva a
> téridőgeometriát, a deformált zárt csapdázott felület még mindig zárt
> csapdázott felület marad). A definició mögött az a kép van, hogy a felület
> olyan erős gravitációs centrumot zár körül, ami már a kifele induló fényt
> sem engedi tovaterjedni. Ilyen felületek pl. a Schwarzschild téridő $0 < r
> < 2m$ tartományának az $r=const$, $t=const$ felületei is. Bizonyitható
> [4], hogy ilyen felületek az anyag elég kis tartományba való
> koncentrálásával is létrejönnek.
>
> Hogy e fogalom mennyire jól ragadja meg a fekete lyukak lényegi
> tulajdonságát, azt a [2] publikációban bizonyitott és e fogalomra épülő
> tétel, azaz Penrose szingularitástétele, mutatja:
> Ha
> (1) az Einstein egyenletek teljesülnek,
> (2) az anyag energiasűrűségét minden megfigyelő nemnegativnak látja,
> (3) a téridő geometriája és az anyagmezők értékei egy teljes, nemkompakt
>      térszerű hiperfelületen (ún. Cauchy felületen) megadott kezdeti
>      adatokból megjósolhatók,
> (4) a téridőben van egy zárt csapdázott felület,
> akkor a téridő tartalmaz olyan fényszerű geodetikust, ami nem értelmezett
> az affin paraméterének a tetszőlegesen nagy értékére.
> Más szóval, ez a geodetikus *véges* affin paraméterhosszon belül kifut a
> téridő peremére; vagyis az ilyen téridők határpontjai között vannak
> olyanok is, amelyek a téridő belső, reguláris pontjaitól *véges* affin
> távolságra vannak. Ezek a szingularitások.
>
> A csapdázott felület fogalmának a bevezetése és a most idézett tétel
> bizonyitása valódi *paradigmaváltást* is jelentett a gondolkodásunkban és
> új matematikai eszközöket hozott az általános relativitáselméletbe. Ez
> elsősorban a topológia, differenciáltopológia és a globális
> differenciálgeometria fogalmainak és módszereinek az egyre kiterjedtebb
> alkalmazását eredményezte. Az új módszerek lehetővé tették olyan kérdések
> megválaszolását is, amelyek a korábbi technikákkal, pl. a
> differenciálegyenletek lokális analizisével, nem voltak megválaszolhatók.
> Ezen globális topológiai/geometriai módszereket mutatja be Penrose immár
> klasszikusá vált s a szakma alapművének tekinthető [5] dolgozata. Ezzel
> Penrose egy új iskolát teremtett a modern általános relativitáselméletben.
> Hawking és Ellis [3] monográfiája is nagyban ezen alapul.
>
> Penrose [2]-beli klasszikus szingularitástételét öt évvel később Hawking
> és Penrose általánositotta ill. terjesztette ki kozmológiai
> szingularitások létét is megjósló tétellé [6], az [5]-beli globális
> technikák teljes tárházának egy parádés alkalmazásaként.
>
> Eredetileg a téridő szingularitásait az Einstein egyenletek egzakt
> megoldásaiban úgy azonositottuk, hogy azok a téridő peremén lévő, de a
> téridő reguláris pontjaitól véges távolságra lévő azon `pontok' (vagy épp
> `felületek'), ahol a görbület valamilyen módon végtelenné válik. A Penrose
> és Hawking--Penrose-féle szingularitástételek az eredeti formájukban
> azonban semmit nem mondanak a görbület viselkedéséről. Csak annyit
> garantálnak, hogy a perem pontjai között vannak olyanok, amelyek a belső
> pontoktól véges affin távolságra vannak, de azt már nem, hogy az e
> pontokba futó geodetikusok mentén a görbület divergál. Meglepő módon egy
> ezzel épp ellentétes irányba mutató eredmény származtatható: megmutatható
> [7], hogy mind a Penrose, mind a Hawking--Penrose (valamint a [3]
> monográfiában található további három) szingularitástétel bizonyitása
> módositható oly módon, hogy a tételek eredeti feltételei nem csak a
> szingularitásokba futó geodetikusok létét garantálják, hanem azt is, hogy
> ezek mentén a görbületnek a geodetikusok által meghatározott komponensei
> *nem* divergálhatnak akármilyen gyorsan. A Penrose-féle szingularitástétel
> jelentőségét, tanulságait is áttekintő és csaknem teljes irodalomjegyzéket
> adó viszonylag friss összefoglaló cikk a [8] publikáció.
>
> Végül, a teljesség kedvéért meg kell jegyeznünk, hogy a fekete lyukak
> kapcsán Hawking vitte végig a Penrose által kezdett paradigmaváltást: a
> hetvenes évek elején ő definiálta matematikailag is az eseményhorizontot,
> amelyről bizonyitotta, hogy az egy olyan tartományt zár körül, ami
> tartalmazza az összes zárt csapdázott felületet [3]; és hogy az
> eseményhorizont úgy viselkedik, mint egy termodinamikai rendszer,
> kielégitve a termodinamika főtételeivel analóg tételeket [9]. S hogy a
> fekete lyukak ezen viselkedése nem csak *analóg* a termodinamikai
> rendszerekével, hanem ezek *valódi fizikai* hőmérséklettel rendelkeznek, a
> Hawking sugárzás néhány évvel később megjósolt jelensége mutatja [10].
>
> Stephen Hawkingnak is ott lett volna a helye a most dijazottak között. (De
> akkor ki maradt volna ki?)
>
>
> [1] Kovács József, Fekete lyukak kutatói kapták a fizikai Nobel-díjat
>          2020-ban, Magyar Tudomány, 2021/02
>          https://mersz.hu/hivatkozas/matud202102_f54392#matud202102_f54392
>
> [2] R. Penrose, Gravitational collapse and space-time singularities,
>          Phys. Rev. Lett. vol 14, pp 57?59 (1965)
>
> [3] S. W. Hawking, G.F. R. Ellis, The Large Scale Structure of Spacetime,
>          Cambridge Univ. Press, Cambridge 1973
>
> [4] R. Schoen, S.-T. Yau, The existence of a black hole due to
>          condensation of matter, Commun. Math. Phys. vol 90, pp 575 (1983)
>
>      P. Bizon, E. Malec, N. \'O Murchadha, Trapped surfaces due to
>          concentration of matter in spherically symmetric geometries,
>          Class. Quantum Grav. vol 6, pp 961 (1989)
>
> [5] R. Penrose, Techniques of differential topology in relativity, SIAM,
>          Philadelphia 1972
>
> [6] S. W. Hawking, R. Penrose, The singularities of gravitational collapse
>          and cosmology, Proc. Roy. Soc. Lond. A, vol 314, pp 529 (1970)
>
> [7] L. B. Szabados, On singularity theorems and curvature growth, J. Math.
>          Phys. vol 28, pp 142 (1987)
>
> [8] J. M. M. Senovilla, D. Garfinkle, The 1965 Penrose singularity
>          theorem, Class. Quantum Grav. vol 32, (2015) 124008
>
> [9] J. M. Bardeen, B. Carter, S. W. Hawking, The four laws of black hole
>          mechanics, Commun. Math. Phys. vol 31, 161 (1973)
>
> [10] S. W. Hawking, Particle creation by black holes, Commun. Math. Phys.
>          vol 43, 199 (1975)
>
>
> %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
>
> Szabados László
> (Wigner Fizikai Kutatóközpont,
> Elméleti Osztály)
>
>
> *-----------------------------------------------------------------------*
> |             A FIZINFO a fizikus informacios rendszer resze            |
> |                                                                       |
> |     Cikk, hozzaszolas a                                               |
> |                                                                       |
> |                         fizinfo AT lists.kfki.hu                         |
> |                                                                       |
> | cimre  kuldheto.  Ilyenkor  a subject-sorba a cikk cimet kell irni.   |
> | A cikk szovege a level torzse. Ez sima szoveg legyen!                 |
> |                                                                       |
> | Informacio: https://mailman.kfki.hu/sympa/info/fizinfo                |
> |                                                                       |
> | A  beerkezo  levelek feldolgozasat program vegzi. Az emberi valaszt   |
> | igenylo kerest, kerdest az alabbi cimre lehet megirni:                |
> |                                                                       |
> |                                          listsadm AT mail.kfki.hu        |
> |                                                                       |
> *-----------------------------------------------------------------------*
>
>
>
>
>
>